9大因素阻碍你在社会媒体上的成功 （转）

不管他们的现状如何，大多数部落客都希望自己在社会媒体上得到更多关注。然而很可惜，只有很少一部分人获得显著成果。如果你想在社会媒体上有所成就，那么你一定要了解并解决以下这些阻碍你发展的因素。

1. 缺少关系网

大多数部落客初次使用社会媒体时，都不再把他们的文章贴到像“掘客“这样的社会媒体网站上，导致他们得到很少的一点投票。在这一点上，反观那些得到成百乃至上千投票的人，而你的帖子乏人问津，当然要想想是怎么回事了。

要在社会传媒网站上得到关注的关键之一就是建立一个关系网络。掘客网是出了名的偏爱那些朋友众多的用户（尽管这一点在算法程序改动后有了些许改善）。

一个强大的关系网对于你写部落格的几乎每个方面都有帮助，在社会媒体上也一样。在多个方面你的关系网会帮你在社会媒体上小露锋芒。第一，关系网成员比其他人更倾向于给你的帖子投票。

我经常使用社会媒体，我要第一个承认，和部落客的关系会影响我的投票决定。我想，这只是人的本性，总是希望自己的朋友得到好处。所以，建立一个强大的关系网络会让别人找机会也要给你的帖子投票。

第二，很多社会媒体网站都设有和朋友分享链接的功能。StumbleUpon’s share feature工具的共享功能可以通过工具列直接使用。掘客网的推荐系统也被掘客们广泛使用。你的朋友越多，关系越好，在你非常需要时，你就有更多的拉票机会。还有，很多部落客通过电子邮件或者IM来拉票。

第三，你的关系网会影响到部落格的总阅读量。那些保持良好关系网的活跃用户，很容易就会拥有众多热烈响应的读者。这些读者不需要你的提醒也会倾向于给你的帖子投票。在很多部落格上你都能看到一个小按钮（像“挖一下”）或者链接，这些都是方便让读者们来投票的。

如果你还在努力在社会媒体上建立一些声望，先看看你的交往习惯吧。你有积极去认识其他部落客和社会媒体用户吗（这可不是在掘客网或者StumeUpon上加几个好友那么简单）？


2. 缺少计划

在社会媒体上的推销和在其他任何领域的推销一样，都要求推销策略和执行技巧。如果你现在的计划就只是发表一些帖子，然后满怀希望的等着大把大把的投票，那可不是个真正的计划。

你在社会媒体上的推销计划取决于你想要实现的目标。社会媒体上推销的最明显的成果就是流量，但是如果流量不能带来其他的东西，也就没有什么意义了。不然，你只不过就是榜上有名了几天，但是这并没有什么真正的价值可言。

你是想通过社会媒体来吸引消费者吗(很难，但不是没可能)? 还是你想建立一个链接？是通过社会媒体让你或者你的部落格出名？不管你的目的是什么，重要的是弄清楚你的重点是什么，然后做出计划来实现它。

你的计划还要涉及在社会媒体上采用什么类型的帖子。你要使用信息帖吗？资料列表？辩论？幽默笑话？新闻？你要找到最能帮助你实现目标的那一种。

具体选择哪些社会媒体网站也是计划之一。在成百上千家网站之中仅有效地选择选择几家并不容易。为了得到最好的结果，你要成为这些网站的活跃用户，从而了解不同网站的读者和最有效果的帖子类型。然后你就可以针对特定的读者群发表帖子了。


3. 缺少读者

如果没人读你的帖子，也就没人给你投票。上面我提到过建立关系网会帮助你获得更多读者的投票。我相信你也一定注意到了，大多数列入掘客网头条的文章都是来自大网站（比如TechCrunch，Gizmodo, Smashing Magazine等等）。

比起一个只有百来个读者的小部落格，这些拥有大量读者的网站更容易得到投票。小部落格很不幸。但是如果你没有大量的读者，想要在社会媒体上取得成功会更艰难。这并不意味着你无法在社会媒体上取得好的成就，但是的确意味着要更好的取得成就，你必须努力扩大你的读者群。


4. 缺少合适内容

帖子内容本身是在社会媒体上不能取得成功的一个直接原因。当我刚开始使用社会媒体时，我发表的那点东西根本不对读者的胃口。并不是所有的内容都能吸引社会媒体上读者的注意力。帖子不单是要有高质量的内容，还要对其他用户产生吸引力。

如果你在社会媒体上是个新手，花点时间浏览下热门的帖子，从这些易于得到响应的帖子里看看你能学到什么。想想看怎么把这些用在你自己的帖子里。关于你自己的部落格你有什么创意也能吸引这些读者？


5. 强行发表无关内容

之前我提到过，并不是所有的帖子在社会媒体上都能有作用。如果你企图强行发表帖子，你可能什么也得不到。在我使用的一些定位于网页设计和发展的社会媒体上，总能看到一些格格不入的帖子。这些帖子从来就不能上头条，也永远也不会有机会被人关注。对于发帖子的人来说，这就是在浪费时间。

如果把你的每一篇帖子都发到社会媒体上，那也是强行发表。不可能每一篇帖子都适用于社会媒体。如果某个帖子不太可能成功，就不要强行发表了。等到你有非常合适的帖子再发表，效果会好的多。


6. 缺少中心

你的社会媒体推销计划很重要（见第二点），同时将精力集中于你的计划上也很关键。时间长了，你很容易就为社会媒体上的数字分心了，而忘了你的计划中心是什么。

我想，一个总是努力争取在掘客网登上头条的部落客就是典型的例子。你在很多其他网站也能很容易就取得成功，但是忽略了中心计划，只是追求在掘客网上的流量，你会毫无成果。


7. 缺少时间安排

很多只关心社会媒体流量的部落客都忽略了时间安排。大多数人很早就看出来部落格的流量在周末通常都会比较低，在社会媒体上这一点同样适用。因此，如果你的帖子是在周末上的头条，比在工作日上头条获得的关注和流量要少些。另一方面，周末来社会媒体的部落客要比平时少，上头条的机会也就大些。

我还发现不同时间段会影响社会媒体的流量。我把部落格发表在美味网，发现在美国，工作时段的头条比非工作时段的头条带来的流量更多。

时间安排是很难控制的（控制你何时发表一个帖子很容易，但是控制这个帖子何时成为头条就得另当别论了）。然而，你应该考虑考虑时间的安排。做些测试，看看怎么样比较适合你。


8. 找错发帖人

在很多社会媒体网站，根据发帖用户的声望高低，帖子获得成功难易有别。如果是这种情况，找个声望高的用户来发你的帖子，会给你的成功增加很大的机会。可能你的朋友声望很高，或者你自己的声望就很高。如果你的目标是掘客网，你可能需要特定的某个人来发表你最好的帖子，否则，如果你找个声望很低的人来发表你有望上头条的帖子，风险会很大。


9. 缺少有力标题

要在社会媒体网站上脱颖而出是相当困难的，因为有那么多的帖子都为吸引众人眼球在竞争。你标题的有多有力，会很大地影响到有多少人来点击和多少人会投票。

不仅仅是你的部落格标题很重要，你的发表帖子的标题也很重要。大多数情况下两者是一样的，但是有时候你会看到，精明的社会媒体用户会换一个名字，使之更见引人注目，而这一点将大大的帮助增加成功机会。


你有什么样的经验？

关于在社会媒体中如何取得成功，你还注意到什么关键因素了吗？

支持非IE浏览器真的那么难吗？（转）

<转自：http://www.kenengba.com/post/774.html>

支持非IE浏览器真的那么难吗？

写于2009-03-20 – 9:52 下午 | 作者:Jason Ng | 类别 » 互联网络 |

微软最近推出了IE8正式版。当你知道上网需要的是浏览器，而不是那个"e"时，你一定知道，不管IE推出什么版本，只要它的核心不变，它一直是个“老掉牙”的浏览器。我在twitter里讽刺了它一句。

国内的非IE浏览器使用者正在不断增加，当使用Firefox或Safari浏览网银的时候，你必定会感到沮丧：已经到了支付这一步了，偏偏要用IE重新开始？我们不禁会问，支持非IE浏览器真的那么困难吗？

浏览器性能对比：

一、滞后的中国互联网

1、跟随模仿思想

自从第二次工业革命之后，可以说中国并没有太多的创新出现，它一直跟随着其它国家的步伐。基本上我们的思想是：别人能做到的，我们也能。

但事实上我们缺乏一种思想：别人没有想到的，我们可以想到。

你并不需要总是跟着别人走，否则，你总是会落后其他人。计算机业就是一个好例子。曾经有人说，中国的互联网滞后美国的5年，当然这个滞后并不是说总体的滞后，是平均水平的滞后。

腾讯不是一个模仿高手么？它在中国找到了出路，理解中国网民的需求。如果它是一家美国公司呢？

创新思想的缺乏原因不是单方面的，Web2.0Share写了一篇关于创新的思考。

2、安于现状的思想

中国人并不太喜欢追求改变，安于现状是大多数人的追求。这也是为什么自从89年发生了一场事件后，久久不见类似的事情发生。

这种安于现状的思想延续到了计算机、互联网上面。

为什么还有那么多人用智能ABC而不用搜狗拼音？为什么还有那么多人用IE6？

因为在一些人的思想里，他们不追求更好的，不想去适应一个新的事物。

3、但求安稳的思想

跟随模仿、安于现状，根本上体现了一种求稳定不求更好的思想。

同样的，这种思想已经渗透到中国互联网，导致各种服务的迁移成本巨大，用户不能选择更好的服务。

4、前面3点与非IE浏览器有什么关系？

我猜你一定会发出这样的疑问。

当我敲起键盘时，我第一个想到的不是为什么还有那么多人用IE6，而是不求变更的思想。

这种不求变更的思想，或者说但求安稳的思想，直接导致了IE、或者说IE6的长期存在。不是说IE份额过载只出现在中国，而是在中国特别严重，除了和网民的素质有关外，和根植于中华民族的思想也有很大关系。

这些思想的泛滥，不但导致了社会落后、封闭、和谐，还延伸到了互联网上面，导致“甘于低效、居安不思危”。

二、使用IE6的理由

没有一个web设计师是最喜欢IE6的，甚至没有一个web设计师是喜欢IE6的。

IE6的存在让网页制作者感到头疼，他们不得不妥协来让网页兼容IE6，或专门为IE6写不同的CSS。

我十分羡慕Techcrunch的浏览器份额，第一位的是Firefox。而在国内，绝大多数网站的浏览器份额里，IE6 100%是占据第一位的。理由可能如下：

1、盗版XP携带IE6

毫无疑问中国的windows操作系统大多数是盗版的，同时，大多数是XP。而往往这些盗版XP携带的是IE6浏览器。

2、不使用windows自动更新

由于担心自己的盗版XP失效，或出现“黑屏”，很多人将系统的自动更新关闭了。因此它们也收不到IE的升级通知。

实际上IE7后来是取消了正版验证的。

3、上网只认"e"图标

我不得不说一个冷笑话：

上个星期有一个朋友打电话我，说她的电脑上不了网。

“QQ能上去吗？”

“能”

“其它浏览器能上网吗？”

“什么是浏览器？”

“除了那个'e'图标的程序”

……

这个冷笑话告诉我们：很多人并不知道这个世界还有其它浏览器，甚至不知道上网的那个东西叫浏览器。

4、不求改变的思想

实际上很多人知道有其它浏览器存在，但不愿意去尝试，不愿意做出改变。

或许是因为没时间，但必须说，用IE6会更让你损失时间。使用其它浏览器虽然需要一段很短的适应过程，但为的是节省你以后的时间，提高你的浏览体验和办事效率。

5、错误地理解其它浏览器

为什么我用firefox打不开某某网页？为什么我在Opera里播放不了音乐？ Chrome就是个垃圾浏览器！……

这样的话语不时出现在我耳边，我不得不重复一遍又一遍告诉我的朋友：这不是浏览器的问题，不是浏览器垃圾，是这个网站垃圾。

三、没有远见地适应

在“关于AV我所知道的一切与思考”里曾经说过，之所以有AV，是因为有这个需求。

将这个理论套用到网银里，反过来说：之所以不支持非IE，是因为目前没这个需求。

但偏偏有一些银行做无力的推托，比如北京银行给一个询问为什么该银行不支持Firefox的回复：

1、Firefox作为一种开源的浏览器，要求开发的语言必须具有通用性，虽然firefox可以添加许多安全插件，但由于一些插件是第三方开发的，所以语言的差异性就更加的显著，很有可能造成浏览时出现问题。

2、Firefox为了兼容windows，linux，unix和maxos，必须制作一种统一的 浏览器内核，而实际上，这些操作系统的网页浏览方式是不一样的，所以在css，javascript，vbscript等网页脚本语言的调用方式上也是不 同的，因此，在用非IE的浏览器上使用网上银行会出现样式错乱或者使用出错的情况。

3、原来的网银系统使用的框架主要是静态jsp实现方式，仅仅应用了很少的样式结构，所以，对于浏览器的兼容性基本没有影响。但是新的网银系统使用了较多的css和较高版本的js，所以会出现对于firefox不兼容的问题。

鉴于上述原因，我们建议你使用系统自带的IE浏览器。　

这些理由都是苍白无力的，它只是不想说出根本原因：中国大多数人用的都是盗版XP，什么叫浏览器都不知道，肯定都用IE，支持其它浏览器？那不是浪费我们的钱财么？！

不得不说，这又是一种互联网滞后的表现。

四、网银真的不能脱离IE吗？

非也，linuxbacks.cn做了一张网银非windows平台兼容性列表：

银行	业务	网上支付	网上转帐	网上查询
浦东发展银行	东方借记卡	支持	支持	支持
	浦发信用卡	支持	支持	支持
广东发展银行	广发理财通卡	支持		支持
兴业银行	借记卡	不支持	不支持	不支持
中信银行	所有银行卡	不支持	不支持	不支持
中国银行	长城借记卡	不支持	不支持	不支持
	长城人民币信用卡	支持	支持
	长城国际信用卡	国内不支持	不支持	支持
招商银行 交通银行 中国农业银行 中国工商银行 中国建设银行 光大银行 民生银行 华夏银行 渤海银行 北京农村商业银行 南京银行 顺德农信社 上海农村商业银行	所有银行卡	不支持	不支持	不支持

你可以看到，网银支持非IE不是没有可能，浦发银行完美地支持了非IE浏览器。

从表中可能看到，四大银行几乎都是清一色的IE Only的，或许和中国移动一样，赚的钱最多，做的事最少，这就是它们的逻辑。

五、让你的网站脱离IE Only体系

这不是恐吓你，如果你的网站还是IE Only，请马上作出修改。不要拿IE的错理解成对的，不要把非IE浏览器的对理解成错的。

目前的趋势是：

1、非windows用户越来越多

2、非IE系用户迅速地增加

3、网页设计越来越趋向于标准化，而不是IE化

现在的网页不再是简简单单的文本和图片，还有大量的多媒体和JS，IE根本无法承受得起，因此它经常假死。

(pic via)

作为一个web设计者，不应顺着用户守旧的习惯，IE已经没有前途了，或许你应该告诉IE使用者：你可以用一个更好的浏览器浏览我们的网站。

查看库中的函数（objdump）

看 Linux C 语言编程的时候经常遇到些不认识的函数，在编译的时候需要连接库文件。但是却不知该连接哪个库，动用 nm 提示的却是 "no symbols"。解决办法是用 objdump，nm 的 man 文件中的 "See also"，属于 binutils 成员。

$ objdump -T *.so

就能看到什么库文件中含有相应的函数了。

从“迷失的8”到生成函数：小数展开的秘密（转）

转自 matrix67.com：<http://www.matrix67.com/blog/archives/1574>

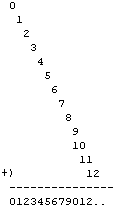
小学时经常在计算器上面按12345679这个神秘的8位数。这个数牛就牛在，它乘以9的结果正好等于111111111。你可以在计算器 上输好12345679，然后问MM“你的幸运数字是多少”；如果她说“7”，你就在计算器上按“乘以63”，计算器上将会显示出清一色的7字，看上去无 比壮观。
假如123456789×9=1111111111的话，我倒不会觉得奇怪。网上流行过一个火星帖子，写了一大堆诸如111111111 * 111111111 = 12345678987654321的式子来展示数学之美，以至于大家会认为123456789×9的结果也一定是一串很有规律的数字。因此，如果我不在 这里说一句123456789×9其实并不等于1111111111的话，估计很多人都发现不了问题。事实 上，123456789×9=1111111101，偏偏就差一个“1”。而怪就怪在，去掉被除数中的数字“8”，偏偏又有了 12345679×9=111111111，一个极其别扭的算式反而得到了完美的结果。不要让你的直觉被数学之美所蒙蔽，数学上有大量出人意料的、看上去 很不对称的结论。
为什么偏偏要少一个“8”呢？难道这真的是算术中的一个不可抹去的疤痕？我们急需要寻求一个解释，填补上算术中的这个不和谐的“漏洞”。一种解释 是，我们看到了123456789×9=1111111101并不美观，想要对其进行改造，进而得到(123456789+1)*9 = 1111111101+9 = 1111111110，于是(123456789+1)*9/10 = 12345679*9 = 111111111。用这种办法的确可以解释“迷失的8”，不过这个解释并不漂亮。为了寻求一个更好的解释，我们来看一看111111111和9的关系。

或许大家都知道，利用等比数列求和，我们可以把任一循环小数还原为分数。111...11和9之间有一个非常精妙的联系：1/9 = 0.111... 。换句话说，1000000000/9取整之后就应该等于111111111。而这个神秘的12345679，就应该是1000000000/81取整后 的结果了。1/81到底等于多少呢？拿精度稍微高一点的计算器一算，我们发现1/81 = 0.01234567901234... 。原来，12345679的秘密全在1/81里面，12345679*9=111111111其实相当于是拿1/81乘以9，取得了1/9的小数部分。
现在余留的问题就是，为什么1/81的前面几位是.012345679呢？仔细观察这个小数，你会发现整个小数的循环节就是012345679，偏偏就少一个“8”。这到底是为什么呢？
为了解释一种反常的数学现象，一个有趣的思路就是，“如果不是这样，你觉得又该是怎样呢？”理想中，这种有悖于数学之美的事情是不应该发生 的，1/81要是等于0.01234567890123456789...就好了，或者更牛B一点的，有没有可能等于 0.0123456789101112131415...？哦，这个好像太夸张了，后面这个小数明显是一个无限不循环小数，不可能和一个有理数相等。不过 呢，Σn/10^(n+1)倒是有可能的。想到这一点，我们最初的谜题迎刃而解！

原来，“迷失的8”并不是一个算术上的瑕疵。或许1/81的小数部分本来就应该是123456789..，接下去的一个数应该是10，但它 应该占据两个数的位置，而留给它的原本只有一个数位。于是乎，数字10中的个位“0”与“9”的后面一位对齐，而十位“1”则加到了“9”身上并产生了进 位，得到了123456790的结果，产生了“迷失的8”这一错觉。而后，刚才10的个位“0”又加上了紧随其后的11的十位，11的个位又和12的十位 拼成了“2”，如此反复，使得整个小数部分不断地重复012345679这一循环。

1/81=Σn/10^(n+1)这一猜测似乎很合理，究竟对不对呢？这和81又有什么关系呢？只需要注意到1/81=(1/9)*(1 /9)，联想前面我们讲过的东西，我们就得到了一个虽然不严密但是颇有启发性的推理。111*111=12321，是因为111*111相当于把111错 位写成三行后加起来；类似地，前面提到的极端情形111111111 * 111111111 = 12345678987654321也是如此。那么，如果10个1乘以10个1呢？如果无穷个“1”乘以无穷个“1”呢？当我们计算1/9的平方时，我们 实际上在做的正是用无穷多个1去乘以无穷多个1，而乘式的第n+1列里恰有n个“1”，它们加起来并产生适当的进位后就得到了 0.0123456790123... 。

循环小数与整数之间存在着很多微妙的关系。很多时候，利用小数展开我们能解决很多无从下手的算术题目。小学奥数中有一道题目我印象极深：一 个位数小于30的、以“15”打头的整数，把这个“15”移到数的末尾后，新数正好是原数的5倍。问原数是多少。很少有人能想到，解开这道题的钥匙竟然是 分数和小数。假设有某个小数x的循环节就等于我们要求的数，那么

可知100x-5x=15，解得x=15/95=3/19。把3/19还原成小数，发现它的循环节是157894736842105263，问题就如此简单的解决了。
且慢，我还准备了更加精彩的数学魔术！让我们来看一看下面这套把戏：

100/9899 = 0.0101020305081321345590463 ...

牛B吧！两位两位的看，前面几个数正好形成Fibonacci数列！不过，再往后走，位数的限制迫使进位产生，打乱了原有的秩序。能让每个数的位数更长一些吗？能！请看：

1000/998999 = 0.001001002003005008013021034055089144233377610...
10000/99989999 = 0.000100010002000300050008001300210034005500890144...
100000/9999899999 = 0.00001000010000200003000050000800013000210003400055000890014400233...
......................

这个就更加奇怪了。为什么一个简简单单的分数展开之后竟然出现了Fibonacci数列？其实，道理和前面所讲的很相似。100/9899 显然是由100/(10000-100-1)得到的，让我们来看一下0.0101020305081321...乘以(10000-100-1)是否能还 原成100：

可以看到，这个“Fibonacci小数”的10000倍，减去它的100倍，再减去它自身，得到的结果正好是100，究其原因则是Fibonacci数列的递归性质。熟悉生成函数的读者猛地一拍大腿，唉呀！这不就是生成函数么！我在讲解生成函数的日志里曾经写道：

接下来我们要演示如何使用生成函数求出Fibonacci数列的通项公式。
Fibonacci数列是这样一个递推数列：f(n)=f(n-1)+f(n-2)。现在我们需要求出它的生成函数g(x)。g(x)应该是一个这样的函数：
g(x)=x+x^2+2x^3+3x^4+5x^5+8x^6+13x^7+...
等式两边同时乘以x，我们得到：
x*g(x)=x^2+x^3+2x^4+3x^5+5x^6+8x^7+...
就像我们前面说过的一样，这相当于等式右边的所有系数向右移动了一位。
现在我们把前面的式子和后面的式子相加，我们得到：
g(x)+x*g(x)=x+2x^2+3x^3+5x^4+8x^5+...
把这最后一个式子和第一个式子好好对比一下。如果第一个式子的系数往左边移动一位，然后把多余的“1”去掉，就变成了最后一个式子了。由于递推函 数的性质，我们神奇地得到了：g(x)+x*g(x)=g(x)/x-1。也就是说，g(x)*x^2+g(x)*x-g(x)=-x。把左边的g(x) 提出来，我们有：g(x)(x^2+x-1)=-x。于是，我们得到了g(x)=x/(1-x-x^2)。

原来，100/9899说穿了就是把x=1/100代入生成函数g(x)。
这下子就热闹了。考虑数列1, 4, 9, 16, 25, 36, ...的生成函数g(x)=x(1+x)/(1-x)^3，代入x=1/100得到g(1/100)=10100/970299，于是出现了：

10100/970299 = 0.0104091625364964 ...

当然，想要更牛B的也不难：

g(1/1000) = 1001000/997002999 = 0.001004009016025036049064081100121144169 ...

再来看看数列2, 4, 8, 16, 32, ...的生成函数g(x)=2x/(1-2x)，利用它可以产生出

g(1/100) = 1/49 = 0.0204081632 ...

或许有人会恍然大悟，原来，1/7=0.142857...也不是一个巧合。14是7的两倍，28是7的四倍，57是7的八倍加一，这都是因为它们是7乘以“2的幂序列”并产生适当进位后得到的。
重新回到我们先前讨论的话题，我们惊奇地发现，数列0, 1, 2, 3, 4, ...的生成函数为g(x)=x^2/(1-x)^2。于是：

g(1/10) = 1/81 = 0.0123456790123...

Windows 下播放视频文件花屏现象的解决

老爸经常让我给他看看他的 Windows，不知为何无法正常播放许多视频，显示出来的总是好像热断层扫描一样的图像。最终，我在网上找到了答案：

桌面上右击属性 然后点设置 然后点高级 然后点疑难解答 然后拖上面的滑条，拖到无就肯定可以放了（来源：http://bbs.feey.cn/thread-4563-1-1.html）

原来是显卡加速的原因，我把滑块置于第三档就正常，在第四档就花了。也就是说，只要调节到“禁用所有的 DirectDraw 和 Direct3D 加速程序”就能正常播放那些视频了。

查了下 assert.h 的用法

（本文已发布到 http://spidertiger2.blogspot.com/2009/03/asserth.html）

考上机关公勤后，这几天在公司没事，就有空研究起 Linux 下的 C 语言来。之前学得很空泛，不了解所以然，连 gcc 的 -I、-L、-l 都分不清楚，连 makefile 也不会写。于是下载了 GNU 的 coreutils 源代码进行研究。当我看 factor.c 的时候看到了一个奇怪的头文件：

#include <assert.h>

于是就 google 开了，发现 assert() 真是个好东西，可以在调试过程中帮上很大的忙。下面转贴一篇网文（来源：<http://www.cnblogs.com/phonefans/archive/2008/12/24/1361381.html>）：

=========================

assert() 函数用法

assert宏的原型定义在<assert.h>中，其作用是如果它的条件返回错误，则终止程序执行，原型定义：
#include <assert.h>
void assert( int expression );
assert的作用是现计算表达式 expression ，如果其值为假（即为0），那么它先向stderr打印一条出错信息，
然后通过调用 abort 来终止程序运行。
请看下面的程序清单badptr.c：

1 #include <stdio.h>
2 #include <assert.h>
3 #include <stdlib.h>
4 int main( void )
5 {
6 FILE *fp;
7
8 fp = fopen( "test.txt", "w" );//以可写的方式打开一个文件，如果不存在就创建一个同名文件
9 assert( fp ); //所以这里不会出错
10 fclose( fp );
11
12 fp = fopen( "noexitfile.txt", "r" );//以只读的方式打开一个文件，如果不存在就打开文件失败
13 assert( fp ); //所以这里出错
14 fclose( fp ); //程序永远都执行不到这里来
15 return 0;
16 }

已放弃
使用assert的缺点是，频繁的调用会极大的影响程序的性能，增加额外的开销。
在调试结束后，可以通过在包含#include <assert.h>的语句之前插入 #define NDEBUG 来禁用assert调用，示例代码如下：
#include <stdio.h>
#define NDEBUG
#include <assert.h>
用法总结与注意事项：
1)在函数开始处检验传入参数的合法性
如:
1 int resetBufferSize(int nNewSize)
2 {
3 //功能:改变缓冲区大小,
4 //参数:nNewSize 缓冲区新长度
5 //返回值:缓冲区当前长度
6 //说明:保持原信息内容不变 nNewSize<=0表示清除缓冲区
7 assert(nNewSize >= 0);
8 assert(nNewSize <= MAX_BUFFER_SIZE);
9
10 }

2)每个assert只检验一个条件,因为同时检验多个条件时,如果断言失败,无法直观的判断是哪个条件失败
不好: assert(nOffset>=0 && nOffset+nSize<=m_nInfomationSize);
好: assert(nOffset >= 0);
assert(nOffset+nSize <= m_nInfomationSize);

3)不能使用改变环境的语句,因为assert只在DEBUG个生效,如果这么做,会使用程序在真正运行时遇到问题
错误: assert(i++ < 100)
这是因为如果出错，比如在执行之前i=100,那么这条语句就不会执行，那么i++这条命令就没有执行。
正确: assert(i < 100)
i++;


4)assert和后面的语句应空一行,以形成逻辑和视觉上的一致感
5)有的地方,assert不能代替条件过滤

==================

呵呵，真棒！